Ecuación de la función y sus variables

Definiciones fundamentales

En este sentido, también puede optarse por delimitar esta revisión teórica a tres nociones específicas: Conjuntos, Correspondencia entre conjuntos y Funciones matemáticas, por encontrarse directamente relacionadas con los elementos de la función, que se estudiarán posteriormente. A continuación, cada una de estas definiciones:

Los conjuntos

Por consiguiente, se comenzará por decir que los Conjuntos han sido explicados por las distintas fuentes matemáticas como la agrupación de elementos, que se caracterizan por responder a la misma naturaleza. Por ende, los Conjuntos matemáticos pueden ser entendidos entonces como colecciones abstractas de elementos homogéneos.

Otra característica de este tipo de colecciones será la de estar constituida por elementos, que cuentan con la capacidad de definir al conjunto que conforman, de manera única y exclusiva. Con respecto a la forma de expresión con la que debe contar el conjunto, los diferentes autores han señalado que siempre los Conjuntos deberán ser nombrados por una letra mayúscula, mientras que sus elementos deberán escribirse como una enumeración, separados por comas, y comprendidos entre signos de llaves: { }.

Correspondencia de conjuntos

Así también, dentro de los distintos conceptos que deberán revisarse, se encuentra el de Correspondencia entre conjuntos, la cual ha sido definida como la relación matemática que existe entre dos colecciones, toda vez que uno, algunos o todos los elementos de una colección encuentran correspondencia, según un criterio específico, con los elementos de otro conjunto. Un ejemplo de este tipo de relación puede ser el siguiente:

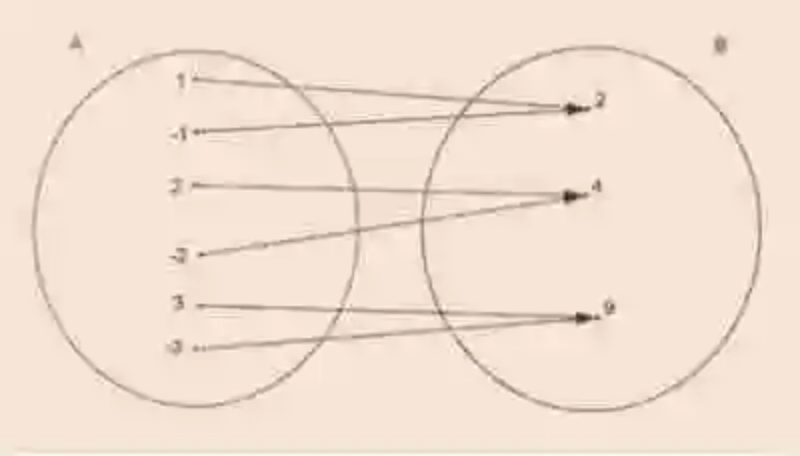
En este caso, se puede ver entonces cómo los elementos del conjunto A encuentran correspondencia en el conjunto B, en base al criterio de correspondencia “tiene por cuadrado”. Así mismo, es necesario señalar que en toda relación de este tipo, entre conjuntos, se pueden encontrar también tres distintas colecciones, las cuales son explicadas de la siguiente manera:

• Conjunto de partida: también conocido como Conjunto inicial, esta colección se caracteriza por ser de ella de donde se genera la correspondencia, es decir, de donde salen las flechas que indican la relación. Por su parte, los elementos que participan de la relación de correspondencia y que hacen parte de este conjunto reciben el nombre de antiimagen, mientras que ejercen la responsabilidad de ejercer como primer elemento del par de correspondencia. En el ejemplo usado para ilustrarla Correspondencia, el conjunto inicial será el siguiente: A= {1, -1, 2, -2, 3, -3}
• Conjunto de llegada: por su parte, en la Correspondencia también se encontrará el conjunto de llegada, o conjunto final, caracterizado por ser la colección en la cual desemboca la correspondencia, así como las flechas, que cumplen con la misión de señalar esta relación. En cuanto a los elementos que participan de la correspondencia y de este conjunto, las Matemáticas los denomina elementos imagen, al tiempo que les asigna la misión de ejercer como segundo elemento del par de correspondencia. En el ejemplo usado, el conjunto de llegada será B= {2, 4, 9}
• Grafo: finalmente, en la relación de Correspondencia entre conjuntos, podrá encontrarse también la colección denominada Grafo, la cual se encontrará conformada entonces por los distintos pares de correspondencia que se han creado entre los elementos relacionados de ambos conjuntos. Un ejemplo de este tipo de relación será el siguiente: G= {(1, 2), (-1,2), (2, 4), (-2, 4), (3, 9), (-3, 9)}

Función

De igual manera, se lanzarán luces sobre el concepto de Función, la cual ha sido entendida como la relación de correspondencia que existe entre dos conjuntos, toda vez que los elementos del conjunto inicial cuenta con solo una imagen en el conjunto de llegada. Así mismo, las Matemáticas han señalado que en la Función pueden distinguirse dos clases distintas de variables, las cuales han sido explicadas de la siguiente manera:

• Variable independiente: por lo general será bautizada por la letra x. Esta variable puede asumir distintos valores, siempre pertenecientes al conjunto de los números reales.
• Variable dependiente: por su parte, en las Funciones, también podrán encontrarse las variables dependientes, las cuales se bautizarán siempre con la letra y, y dependerán del valor de x, así como del criterio de correspondencia en base al cual se ha establecido la relación. Por ejemplo, si se tienen dos conjuntos, en donde los elementos del conjunto inicial cuentan con una sola imagen, y además la relación se ha establecido bajo el criterio “doble de” se tendrá que y = 2.x Se dice que esta variable está en función de x porque depende del valor de esta.

Un ejemplo de función sería el siguiente:

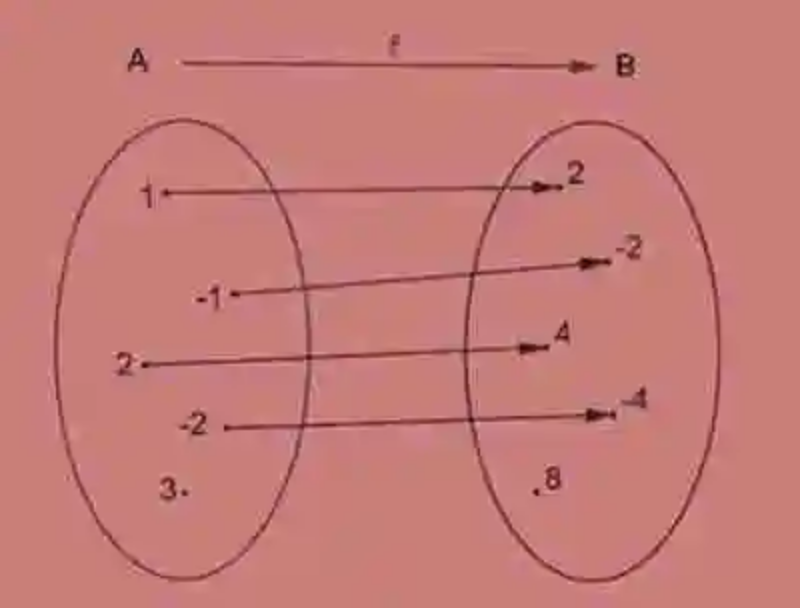
En ella se puede ver cómo cada elemento del conjunto A cuenta con tan solo una imagen en el Conjunto B. Además se sabe que el criterio de relación o correspondencia es “tiene por doble”. Por lo tanto, la Función podría ser expresada de la siguiente forma:

f(x) = y en tanto que y = 2. x

f(1) = 2
f (-1) = -2
f(2) = 4
f(-2)= -4

Ecuación de la función y sus variables

Una vez se han revisado cada uno de estos conceptos, puede que realmente sea mucho más simple aproximarse al concepto de Ecuación de la función, el cual ha sido explicado como el conjunto de operaciones matemáticas a las cuales se debe someter la variable independiente x, a fin de obtener el valor de la variable dependiente y.

Por ejemplo, si se tuviera una función Z, cuyo criterio de correspondencia fuese “el doble de”, entonces se tendría que para obtener la variable y se debería conseguir siempre el doble de la variable x:

f (x) = y →  y = 2.x  → f(x) =  2. x

A esta operación se le conocerá entonces por el nombre de Ecuación de la función, pues es la que permite conseguir las distintas variables por las cuales se establece esta relación matemática entre conjuntos.

No obstante, las Matemáticas también advierten que no todas las funciones se encuentran definidas en base a una ecuación, sino que en algunos casos vienen ya definidas por el Grafo que se establece entre las colecciones relacionadas, es decir, por los pares de correspondencia ya existentes. En este caso, las variables x corresponderán siempre al primer elemento de estos pares, mientras que las variables y serán definidas por el segundo elemento de los pares de correspondencia.

Imagen: pixabay.com