Triángulos en posición de Tales

Definiciones fundamentales

Por consiguiente, se tomará también la decisión de centrar esta revisión teórica en seis nociones específicas: Recta, Segmento, Rectas paralelas, Razón de semejanza, Triángulos y Teorema de Tales, por encontrarse directamente relacionados con los triángulos que se estudiarán posteriormente. A continuación, cada una de estas definiciones:

La Recta

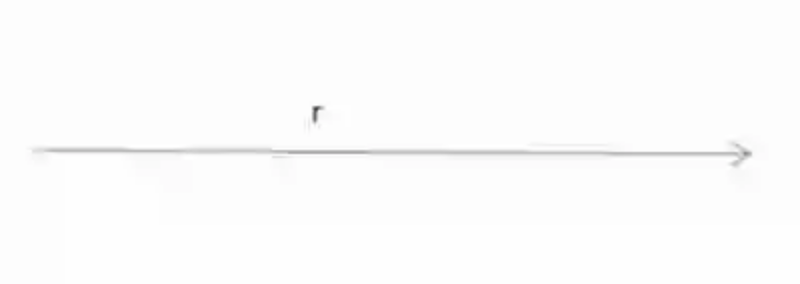
De esta manera, se comenzará diciendo que la Recta ha sido explicada por la Geometría como una figura unidimensional, definida específicamente como una sucesión infinita de puntos, los cuales presentan obligatoriamente la misma disposición.

Así mismo, en términos geométricos, la Recta ha sido explicada entonces como la distancia más corta que existe entre dos puntos, así como la única figura que puede pasar a través de ellos, cosa que puede suceder además tan solo una recta por vez.

Igualmente, la disciplina geométrica señala que en la Recta se pueden encontrar también las siguientes características:

1.- Aun cuando la Recta está compuesta por una sucesión infinita de puntos, que deben tener la misma disposición, ella en realidad puede tener dos distintas direcciones o sentidos, los cuales estarán sujetos a la lectura que se haga de esta figura unidimensional.

2.- De igual forma, estar conformada por esta sucesión infinita de puntos hace que la Recta también sea infinita. Por ende, la Recta no tiene principio ni tiene fin.

3.- Finalmente, la Recta se caracteriza por ser nombrada exclusivamente por una letra minúscula.

A continuación, un ejemplo de Recta:

Segmento

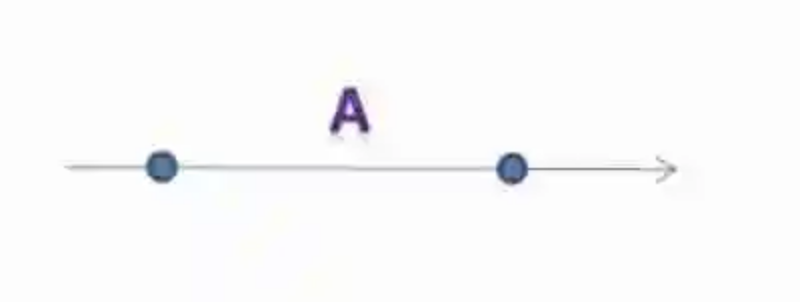
Por otro lado, se deberá tomar también un momento para revisar la definición de Segmento, el cual ha sido explicado por la Geometría como el espacio de una Recta, que queda definido entre dos puntos distintos que son trazados en ella, en algún mundo de su extensión. En consecuencia, al tener un punto de inicio y un punto final, el Segmento se diferencia de la Recta por ser finito.

Así mismo, el Segmento es nombrado con una letra mayúscula. Un ejemplo de Segmento es el siguiente:

Rectas paralelas

Dentro de las distintas definiciones que deben ser abordadas, se encuentra también el de Rectas paralelas, las cuales han sido explicadas entonces como el conjunto de rectas –dos, tres o infinitas- que se ubican en el mismo plano, guardando siempre entre ellas la misma distancia, y sin cruzarse nunca en ningún punto de su extensión infinita. Un ejemplo de Rectas paralelas será el siguiente:

Razón de semejanzas

De igual forma, se deberá lanzar luces sobre el concepto de Razón de semejanzas. No obstante, para esto se debe comenzar por recordar que la Semejanza es la relación de igualdad, que existe entre dos figuras geométricas semejantes, que tienen como características el poseer la misma forma, pero tamaños distintos. Así también, las figuras semejantes tienen lados proporcionales y ángulos iguales.

Por su parte, la Razón de semejanza ha sido explicado por las distintas fuentes como el índice de proporción que existe entre los lados de dos figuras semejantes, toda vez que al dividirse las medidas de ellos, los lados proporcionales arrojan el mismo cociente. Este índice confirma que se trata de dos figuras semejantes. Por ejemplo, si se tuvieran las siguientes figuras:

Y se tratara de establecer la Razón de semejanza entre ellas, se tendría que dividir las medidas de los lados horizontales, y las medidas de los lados verticales. Al hacerlo, se debería obtener en ambas operaciones el mismo cociente:

2 / 3 = 0,66
1 / 1,5 = 0,66

Triángulos

En cuanto a los Triángulos, estos han sido explicados como polígonos de tres lados, es decir, figuras geométricas completamente cerradas, y constituidas por tres segmentos de recta, que se encuentran en puntos específicos.

Así mismo, la Geometría ha señalado que los Triángulos también se distinguen por contar con tres distintos elementos:

• Tienen tres lados, rasgo este que lo definen, en tanto los polígonos se clasifican o se distinguen según el número de sus lados. Los lados del polígono serán siempre rectos.
• Así también presentan tres vértices, estos surgen toda vez que dos lados del triángulo se encuentran entre sí, el vértice es ese punto de unión.
• Por otra parte, los Triángulos cuentan también con tres ángulos, los cuales pueden ser definidos como el espacio geométrico que se encuentra definido los dos lados que coinciden en un vértice. Según las Matemáticas, los ángulos cuentan a su vez con tres elementos: dos lados, un vértice y su amplitud, esta última medida en grados sexagesimales. Los ángulos del triángulo sirven para clasificarlos.

Pese a ser un polígono, los Triángulos se distinguen por ser el único polígono que no presenta diagonales, lo cual sucede porque este polígono no cuenta con vértices opuestos.

Teorema de Tales

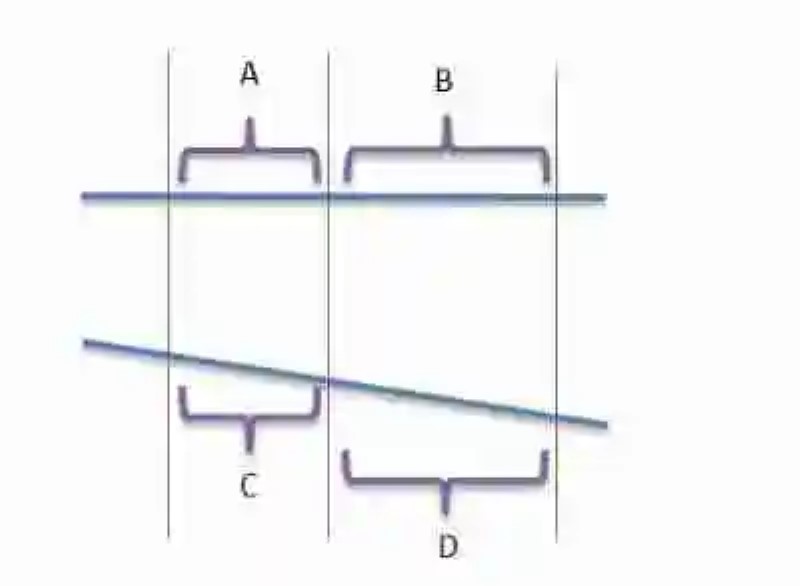
Por último, también será necesario hablar sobre el Teorema de Tales, el cual ha sido explicado entonces como una proposición matemática que señala que siempre que a dos o más rectas  las corte perpendicularmente un conjunto de tres o más rectas paralelas, entonces se generarán en las rectas cortadas segmentos proporcionales entre sí. Por ejemplo:

Si se tuvieran estas dos rectas horizontales, y ellas fuesen cortadas perpendicularmente por estas rectas paralelas, entonces se tendría que se originan los segmentos A, B, C y D. Estos segmentos resultan proporcionales de la siguiente manera:

A y C son proporcionales
B y D son proporcionales

Así mismo, si se dividieran la medida de B entre la medida de A, se obtendría exactamente el mismo resultado que se logra cuando se divide la medida de D entre C.

Triángulos en posición de Tales

Toda vez se han revisado estas definiciones, puede que ciertamente sea mucho más sencillo aproximarse a una explicación sobre los Triángulos en posición de Tales, los cuales pueden ser explicados a su vez como dos triángulos que cuentan con un ángulo en común, y al mismo tiempo los lados opuestos a este ángulo pueden ser interpretados como paralelas que cortan las rectas que sirven de lados contiguos al ángulo en estos polígonos.

Sin embargo, puede que la mejor forma de entender este tipo de triángulos sea a través de la exposición de un ejemplo concreto, como el que puede verse a continuación:

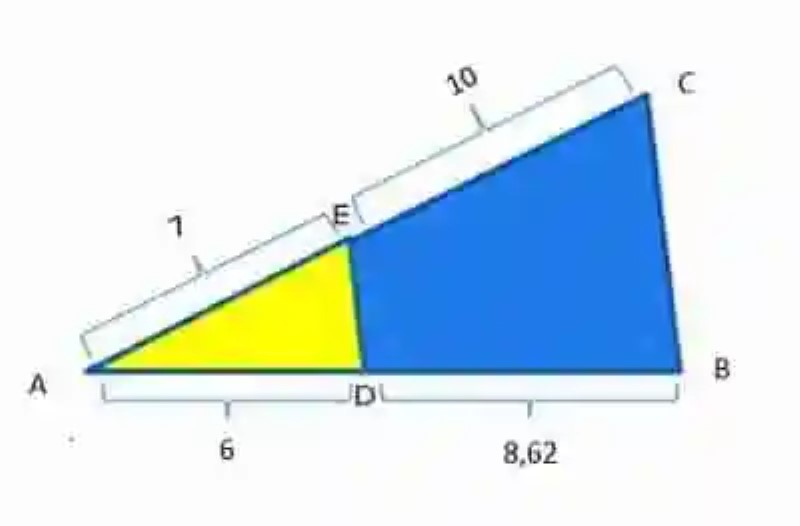
En este caso se tienen dos triángulos: ∆ ABC y ∆ AED. Estos dos polígonos tienen “a” como el ángulo común, mientras que los segmentos ED y CB resultan opuestos a este ángulo. Así mismo, los lados ED y CB constituyen paralelas que cortan las rectas constituidas por los lados AC y AB. Por lo tanto se encuentran en posición de Tales.

Así mismo, los segmentos que se desprenden de este corte resultarán proporcionales entre sí. Por ende, si se dividiese la medida del segmento AE entre la medida del segmento AD, se obtendría el mismo consciente de si se dividiera la medida del segmento EC y DB:

AE : AD = 7 : 6 = 1,16
EC : DB = 10: 8,62 = 1,16

De hecho, si se sumaran las medidas de estos dos segmentos, es decir, si se tomaran los totales de los lados AC y AB, y se dividieran entre sí, se obtendría también el mismo consciente:

AC= 7 + 10 = 17
AB = 6 + 8,62 = 14,62

AC : AB = 17 : 14,62 = 1,1627

Imagen: pixabay.com