Definiciones fundamentales

En este sentido, puede que también resulte prudente delimitar esta revisión teórica a dos nociones específicas: el concepto de fracciones y el de suma de fracciones, por ser estos los elementos y la operación, en base a los cuales surge la propiedad conocida como Elemento opuesto en la suma de fracciones. A continuación, cada uno de ellos:

Las fracciones

Por consiguiente, se podrá comenzar a decir que las fracciones pueden ser consideradas como una forma de expresión de los números fraccionarios, la cual se encuentra conformada por la división entre dos números enteros, cada uno de los cuales cuenta con el nombre y la función que se expone a continuación:

• Numerador: con esta denominación, se conocerá el primer término de la fracción, o dicho de otra forma, el elemento que se encuentra en la posición superior de la fracción. La tarea del Numerador será indicar cuál es la parte del todo que representa la fracción.
• Denominador: en segundo lugar, se encontrará el Denominador, el cual ocupará la parte inferior de la fracción, y que desempeña la tarea de indicar cuál es el todo en base al cual se ha establecido la fracción, como una porción de esta totalidad.

Suma de fracciones

Así también será pertinente tener en cuenta la definición de Suma de fracciones, la cual será entendida como la operación matemática cuyo propósito es combinar los valores de las fracciones que funcionan como sumandos. Sin embargo, la homogeneidad de las fracciones involucradas determinará el método exacto que debe seguirse para resolver estas operaciones, tal como se ve a continuación:

• Si las fracciones coinciden en cuanto a sus denominadores: en primer lugar, puede ocurrir que las fracciones que fungen como sumandos cuenten con los mismos denominadores. En este caso, se sumarán entonces sólo los valores que tengan los numeradores.
• Si las fracciones cuentan con denominadores distintos: por el contrario, si las fracciones que participan en la suma poseen denominadores de distintos valores, entonces de forma previa deberán realizarse las operaciones pertinentes para calcular un común denominador, y entonces proceder con la suma de los numeradores.

Elemento opuesto en la suma de fracciones

Teniendo presente estas definiciones, puede entonces que realmente sea mucho más sencillo aproximarse a una definición sobre el Elemento opuesto que tiene lugar en esta operación. Al respecto, las distintas fuentes coinciden en la importancia de comprender que el elemento opuesto, inverso o simétrico de una operación será aquella fracción que cuente con el mismo valor, pero con el signo contrario, lo cual puede expresarse matemáticamente de la siguiente manera:

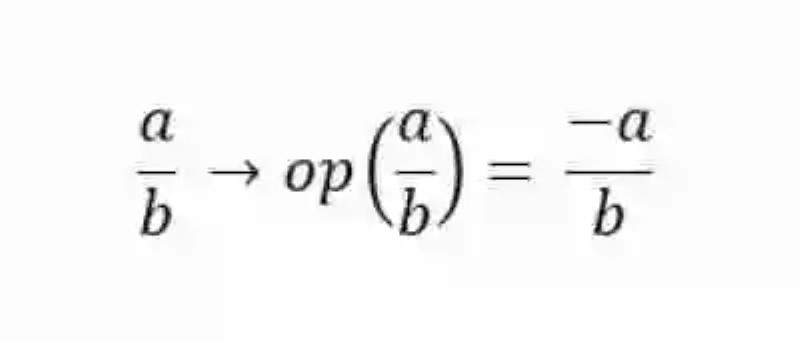
Así mismo, la Propiedad del Elemento opuesto en la suma de fracciones dictará que toda vez que una fracción se sume con su elemento inverso u opuesto, entonces el resultado dará siempre, y sin ningún tipo de excepción, cero. No obstante, puede que todavía sea necesario exponer un ejemplo concreto, que permita ver de forma clara cómo toda vez que una fracción se sume con su inversa da como resultado cero, tal como puede verse a continuación:

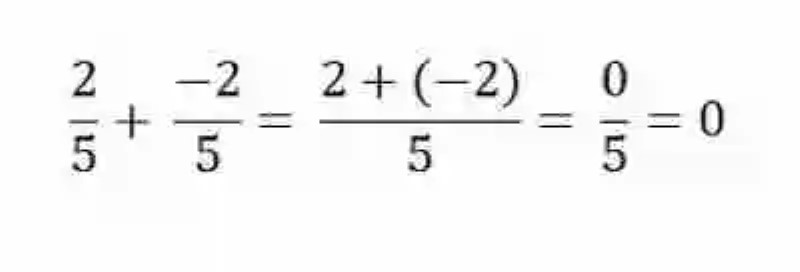
Imagen: pixabay.com